B树深度教学系列(一):磁盘I/O危机 – 为什么二叉树在数据库中失败
从100倍性能差异开始,理解数据库索引设计的底层约束
📝 TL;DR (核心要点速览)
🎯 本篇核心: 磁盘I/O成本是数据结构选择的关键约束
💡 关键发现:
– 性能差距惊人:磁盘访问比内存慢100-10万倍
– 二叉树的陷阱:100万条记录需要20次磁盘I/O
– B树的优势:相同数据仅需3次磁盘I/O
– 根本原因:数据结构必须适应硬件特性
📊 数据对比:
| 存储介质 | 访问延迟 | 相对速度 |
|———|———|———|
| L1缓存 | 1 ns | 基准 |
| 内存(RAM) | 100 ns | 100倍慢 |
| SSD | 100 μs | 100,000倍慢 |
| HDD | 10 ms | 10,000,000倍慢 |
🎓 学习目标:
1. 理解磁盘I/O为何成为性能瓶颈
2. 认识二叉搜索树在数据库中的局限
3. 掌握计算查询成本的思维方式
4. 为下一篇B树原理学习打下基础
🚨 问题的起源:一个看似完美的数据结构
二叉搜索树(BST)的教科书优势
在算法课上,我们都学过二叉搜索树(Binary Search Tree)的优雅之处:
对于n个元素:
- 查找时间复杂度:O(log n)
- 插入时间复杂度:O(log n)
- 删除时间复杂度:O(log n)
1000万条记录?log₂(10,000,000) ≈ 23次比较,完美!
理论上非常美好。但当你把这个数据结构搬到数据库中时,性能却崩溃了。
真实世界的残酷现实
场景: 查询一个拥有100万条用户记录的数据库
SELECT * FROM users WHERE user_id = 123456;
使用二叉搜索树索引的成本计算:
树高 = log₂(1,000,000) ≈ 20
每层需要1次磁盘I/O
总磁盘访问次数 = 20次
如果是机械硬盘(HDD):
- 单次I/O延迟 ≈ 10ms
- 总查询时间 = 20 × 10ms = 200ms
这还只是单个查询!
200毫秒听起来不算太糟?但考虑:
– 数据库每秒可能处理数千次查询
– 用户期望的响应时间 < 100ms
– 还要考虑并发、锁竞争、事务开销
二叉树在数据库场景下彻底失败了。
🔍 深入理解:为什么磁盘I/O是瓶颈
存储层级的性能鸿沟
现代计算机的存储系统是分层的,每一层的速度差异巨大:
详细性能对比表:
| 存储类型 | 典型延迟 | 带宽 | 成本(每GB) | 容量上限 |
|---|---|---|---|---|
| CPU寄存器 | <1 ns | – | – | KB级 |
| L1缓存 | 1 ns | 数TB/s | – | 64 KB |
| L2缓存 | 4 ns | 数百GB/s | – | 512 KB |
| L3缓存 | 10-20 ns | 数十GB/s | – | 几MB |
| 内存(DDR4) | 100 ns | 20-50 GB/s | $10 | 几十GB |
| NVMe SSD | 100 μs | 3-7 GB/s | $0.2 | 几TB |
| SATA SSD | 500 μs | 0.5 GB/s | $0.15 | 几TB |
| HDD | 10 ms | 100-200 MB/s | $0.02 | 几十TB |
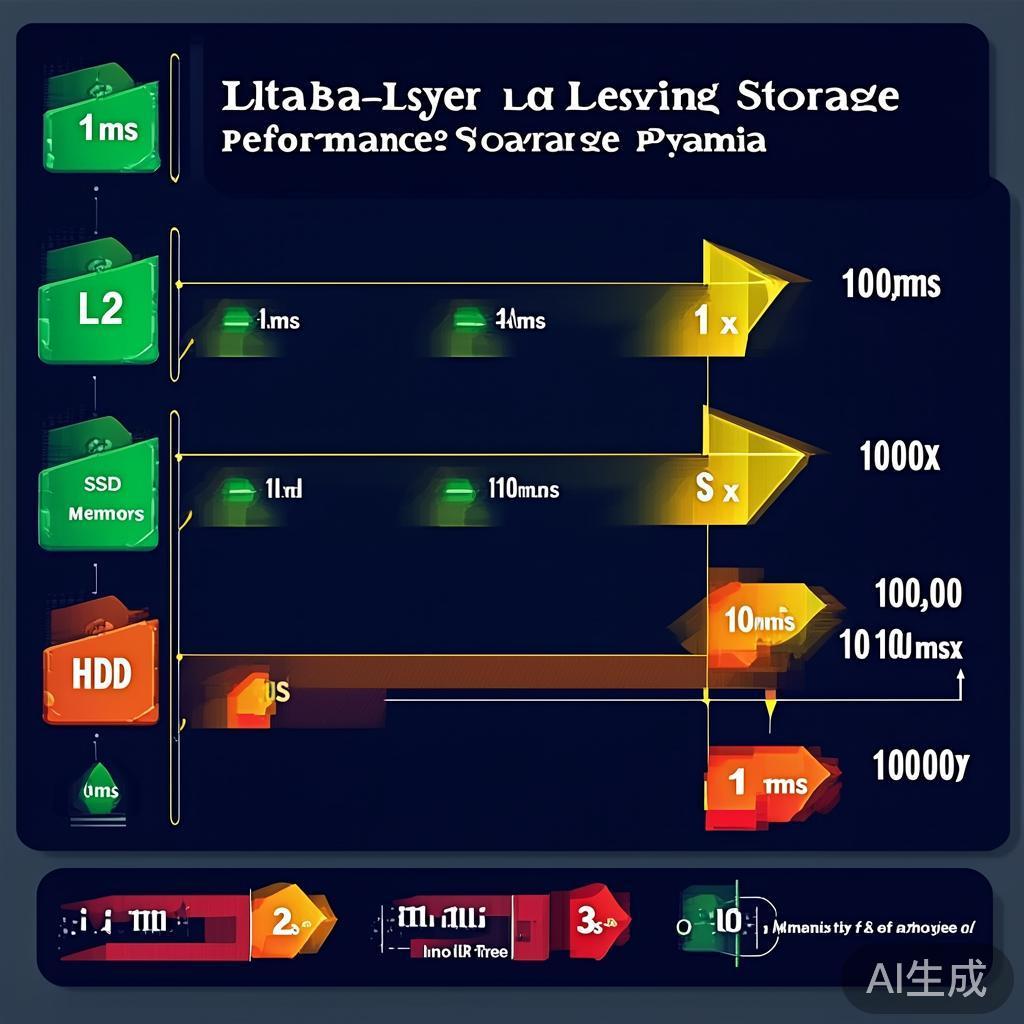
图1:存储层级性能差异对比 – 从L1缓存到机械硬盘的延迟差距
真实数字说话
让我们用更直观的方式理解这些延迟:
时间尺度转换(如果1秒=1秒):
CPU执行一条指令 = 1秒
L1缓存访问 = 3秒
内存访问 = 100秒(1.7分钟)
SSD访问 = 1.16天
HDD访问 = 3.8个月
现在明白为什么一次磁盘I/O如此致命了吗?
💔 二叉搜索树的困境
问题1:树高导致的I/O次数爆炸
二叉树的树高公式:
h = log₂(n)
数据量对比:
- 1,000条记录: h ≈ 10
- 10,000条记录: h ≈ 13
- 100,000条记录: h ≈ 17
- 1,000,000条记录: h ≈ 20
- 10,000,000条记录:h ≈ 23
每增加10倍数据,仅增加约3层。看起来很好?
但问题在于:
– 每层都是一次磁盘I/O
– 磁盘I/O的成本是恒定的(~10ms)
– 树越高,累积延迟越大
问题2:节点利用率低下
二叉树节点结构:
[左指针 | 数据值 | 右指针]
假设:
– 指针:8字节
– 数据值:8字节(仅存储键,不含完整记录)
– 节点总大小:24字节
磁盘块大小:
– 操作系统通常使用4KB页
– 数据库常用8KB或16KB块
空间利用率灾难:
单个4KB磁盘块可容纳:
4096 ÷ 24 ≈ 170个节点
但二叉树每次I/O只读取1个节点!
利用率 = 1/170 ≈ 0.6%
浪费了99.4%的I/O带宽!
问题3:缓存不友好
局部性原理失效:
二叉搜索树的查找路径:
根节点 → 左/右子节点 → 孙节点 → ...
这些节点在磁盘上可能是:
块1 → 块589 → 块234 → 块892 → ...
完全随机访问,无法利用:
- 磁盘预读
- 操作系统页缓存
- 数据库buffer pool的顺序扫描优化
📐 实际成本计算示例
场景:电商网站用户查询
系统参数:
– 用户表:500万条记录
– 使用二叉搜索树索引
– 服务器:配备SATA SSD
查询操作:
SELECT username, email FROM users WHERE user_id = 2847593;
成本分解:
-
计算树高:
h = log₂(5,000,000) ≈ 22.25 → 23层 -
I/O次数:
需要访问23个节点 = 23次磁盘I/O -
延迟计算(SSD):
单次SSD随机读延迟 ≈ 500μs
总延迟 = 23 × 500μs = 11.5ms -
并发场景(1000 QPS):
“`
每秒磁盘I/O需求 = 1000 × 23 = 23,000 IOPS
高端SSD IOPS上限 ≈ 100,000
理论上可行,但考虑:
– 写入操作也需要IOPS
– 其他查询的竞争
– 峰值流量
系统很快会I/O饱和!
“`
成本对比:如果用B树
同样的500万用户,使用B树(扇出=100):
树高 = log₁₀₀(5,000,000) ≈ 3.35 → 4层
I/O次数 = 4次
延迟 = 4 × 500μs = 2ms
性能提升 = 11.5ms / 2ms ≈ 5.75倍
IOPS需求减少 = 23,000 / 4,000 ≈ 5.75倍
这就是为什么所有主流数据库都用B树!
🎯 关键洞察
洞察1:硬件特性决定软件设计
传统算法分析的盲区:
教科书:O(log n) = 很好
现实: O(log n) × 10ms磁盘I/O = 灾难
正确的思维模型:
总成本 = CPU成本 + 内存成本 + 磁盘I/O成本
在数据库场景:
磁盘I/O成本 >> CPU成本 + 内存成本
因此优化目标 = 最小化磁盘I/O次数
洞察2:数据结构的适用边界
| 数据结构 | 最佳应用场景 | 避免场景 |
|---|---|---|
| 数组 | 静态数据、顺序访问 | 频繁插入/删除 |
| 链表 | 频繁插入、内存数据 | 随机访问 |
| 哈希表 | 内存K-V存储 | 范围查询、磁盘存储 |
| 二叉树 | 内存有序集合 | 磁盘存储、大数据集 |
| B树 | 磁盘索引、大数据集 | 小数据集(开销过大) |
洞察3:优化的本质是权衡
二叉树的优势(在内存中):
– 实现简单
– 节点小,内存占用少
– 插入/删除逻辑直观
二叉树在磁盘上失败的原因:
– 为了节点简单性,牺牲了I/O效率
– 为了实现简单,牺牲了空间利用率
– 为了逻辑直观,牺牲了缓存友好性
B树的设计哲学:
– 用节点复杂性换取I/O效率
– 用CPU开销换取磁盘I/O减少
– 用实现复杂度换取性能
🔬 深入一层:为什么不能简单”优化”二叉树
尝试1:增加缓存
想法: 把常访问的节点缓存到内存
问题:
缓存热点数据是有效的,但:
- 冷数据查询仍需完整的磁盘I/O
- 缓存未命中率在大数据集下很高
- 缓存本身有内存开销和管理成本
根本问题没解决:树太高!
尝试2:批量加载节点
想法: 一次I/O读取多个节点
问题:
二叉树的节点在磁盘上分散存储:
父节点 block_123
左子节点 block_456
右子节点 block_789
无法在一次I/O中读取查询路径上的多个节点
除非重新组织磁盘布局,但那就成了... B树!
尝试3:压缩节点
想法: 减小节点大小,让更多节点fit到一个磁盘块
问题:
即使压缩到极致,二叉树的根本限制:
每个节点最多2个子节点
这意味着:
- 树高仍然是O(log₂ n)
- 每层仍然需要单独的I/O
- 本质问题未解决
💡 问题的解决方向
既然二叉树的问题是”树太高”,解决方案自然是:
降低树的高度!
如何降低?
数学推导
树高公式:h = logₐ(n)
其中 a = 分支因子(二叉树中a=2)
降低树高的方法:增大分支因子 a!
示例(100万条记录):
- 二叉树(a=2): h = log₂(1,000,000) ≈ 20
- a=10: h = log₁₀(1,000,000) = 6
- a=100: h = log₁₀₀(1,000,000) ≈ 3
- a=1000: h = log₁₀₀₀(1,000,000) = 2
这就是B树的核心思想:高扇出(high fanout)!
但增大分支因子带来新的挑战:
– 如何在一个节点存储多个键?
– 如何高效查找节点内的键?
– 插入/删除时如何保持平衡?
– 如何选择最优的分支因子?
这些问题,我们将在下一篇《B树基础:扇出如何改变游戏规则》中详细解答。
📊 本篇数据总结
性能对比速查表
| 指标 | 二叉搜索树 | B树(扇出=100) | 改进倍数 |
|---|---|---|---|
| 100万记录树高 | 20 | 3 | 6.7× |
| 查询I/O次数 | 20 | 3 | 6.7× |
| SSD查询延迟 | 10ms | 1.5ms | 6.7× |
| HDD查询延迟 | 200ms | 30ms | 6.7× |
| 磁盘块利用率 | <1% | >50% | 50× |
| 并发支持(QPS) | ~100 | ~600 | 6× |
关键数字记忆
1 ns - CPU指令
100 ns - 内存访问
100 μs - SSD访问
10 ms - HDD访问
100万记录:
- 二叉树:20次I/O
- B树: 3次I/O
🎓 学习检查
完成本篇后,你应该能够:
✅ 概念理解:
– [ ] 解释为什么磁盘I/O是数据库性能瓶颈
– [ ] 说明二叉树在磁盘上失败的三个原因
– [ ] 理解”树高”与查询成本的直接关系
✅ 计算能力:
– [ ] 给定记录数,计算二叉树的树高
– [ ] 估算查询的I/O次数和延迟
– [ ] 对比不同分支因子的性能差异
✅ 决策能力:
– [ ] 判断何时二叉树适用(内存小数据集)
– [ ] 识别磁盘I/O瓶颈的症状
– [ ] 理解为什么需要B树这样的替代方案
🔗 系列导航
本系列文章:
– ✅ 第1篇:磁盘I/O危机 ← 你在这里
– ⏭ 第2篇:B树基础 – 扇出如何改变游戏规则
– ⏭ 第3篇:B树维护 – 分裂、合并与自平衡
– ⏭ 第4篇:生产实现 – MySQL与PostgreSQL的B树优化
– ⏭ 第5篇:替代方案 – 何时放弃B树选择LSM树
下一篇预告:
我们将深入B树的结构设计,解答:
– 如何在一个节点存储多个键?
– 扇出因子如何选择?
– B树如何保证查询、插入、删除都是O(log n)?
– 真实数据库如何实现16KB的B树节点?
📚 扩展阅读
推荐资源
- 经典论文:Organization and Maintenance of Large Ordered Indices (Bayer & McCreight, 1972)
- 深度文章:The Ubiquitous B-Tree (Douglas Comer, 1979)
- 实践分析:MySQL InnoDB存储引擎文档
相关主题
- 操作系统的页缓存机制
- SSD的内部架构和性能特性
- 数据库buffer pool的工作原理
- 索引设计的最佳实践
#数据库索引 #B树 #性能优化 #磁盘IO #数据结构 #后端开发
本文是B树深度教学系列的第一篇,专注于问题的起源和根本约束。理解了磁盘I/O的性能瓶颈,你就理解了为什么现代数据库都选择B树。
下一篇见!





 AI周刊:大模型、智能体与产业动态追踪
AI周刊:大模型、智能体与产业动态追踪 程序员数学扫盲课
程序员数学扫盲课 冲浪推荐:AI工具与技术精选导航
冲浪推荐:AI工具与技术精选导航 Claude Code 全体系指南:AI 编程智能体实战
Claude Code 全体系指南:AI 编程智能体实战
从磁盘I/O角度解释B树的设计动机,这个切入点很好。终于理解为什么数据库不用二叉树了。