B树深度教学系列(二):B树基础 – 结构与查询原理
理解B树如何用”胖节点”和”低树高”解决磁盘I/O危机
📝 TL;DR (核心要点速览)
🎯 本篇核心: B树通过增加节点容量降低树高,从根本上减少磁盘I/O次数
💡 关键发现:
– 核心思想:用”胖节点”换”矮树高”
– 性能飞跃:100万记录从20次I/O降至3次I/O
– 数学原理:树高 = log_m(N),m越大树越矮
– 典型配置:阶数(m) = 200-1000,节点大小 = 4KB-16KB
📊 数据对比:
| 数据结构 | 100万记录树高 | 磁盘I/O次数 | 查询延迟(HDD) |
|———|————|———–|————-|
| 二叉树(m=2) | log₂(10⁶) ≈ 20 | 20次 | 200ms |
| B树(m=100) | log₁₀₀(10⁶) ≈ 3 | 3次 | 30ms |
| B树(m=1000) | log₁₀₀₀(10⁶) ≈ 2 | 2次 | 20ms |
🎓 学习目标:
1. 掌握B树的核心结构设计
2. 理解阶数(m)与树高的数学关系
3. 学会计算节点容量与I/O次数
4. 认识B树在磁盘块对齐上的优化
🏗️ B树的核心设计思想
从问题到解决方案
回顾问题: 第一篇我们发现二叉树在数据库中失败的根本原因:
树高太高 → 磁盘I/O次数过多 → 查询速度慢
log₂(1,000,000) = 20次I/O × 10ms = 200ms
B树的破局之道:
不是减少节点数量,而是降低树的高度!
核心策略:
1. 增加节点容量:每个节点存储多个键(几百个)
2. 增加分支因子:每个节点有多个子节点(几百个)
3. 对齐磁盘块:节点大小匹配磁盘页大小(4KB/8KB/16KB)
直观对比:
二叉树(Binary Tree):
每个节点 = 1个键 + 2个子节点
树高20层 → 20次磁盘I/O
B树(B-Tree):
每个节点 = 100个键 + 101个子节点
树高3层 → 3次磁盘I/O
同样100万条记录,I/O次数减少 85%!
🔍 B树的精确定义
B树的数学定义
一个m阶B树(m-way B-tree)必须满足以下性质:
1. 节点结构
每个节点包含:
[P₀|K₁|P₁|K₂|P₂|...|Kₙ|Pₙ]
其中:
- Kᵢ:关键字(key),按升序排列
- Pᵢ:指向子节点的指针(pointer)
- n:当前节点的关键字数量
2. 阶数约束(Order Constraints)
对于m阶B树:
- 每个节点最多 m-1 个键
- 每个节点最多 m 个子节点
- 非根节点最少 ⌈m/2⌉-1 个键
- 非根节点最少 ⌈m/2⌉ 个子节点
- 根节点最少 1 个键(如果不是叶子节点)
3. 平衡性(Balance)
所有叶子节点在同一层
这确保了查询任何键的路径长度相同
4. 键的排序(Sorting)
对于节点 [P₀|K₁|P₁|K₂|P₂|...|Kₙ|Pₙ]:
- K₁ < K₂ < K₃ < ... < Kₙ
- P₀子树的所有键 < K₁
- Pᵢ子树的所有键在 Kᵢ 和 K_{i+1} 之间
- Pₙ子树的所有键 > Kₙ
具体示例:5阶B树
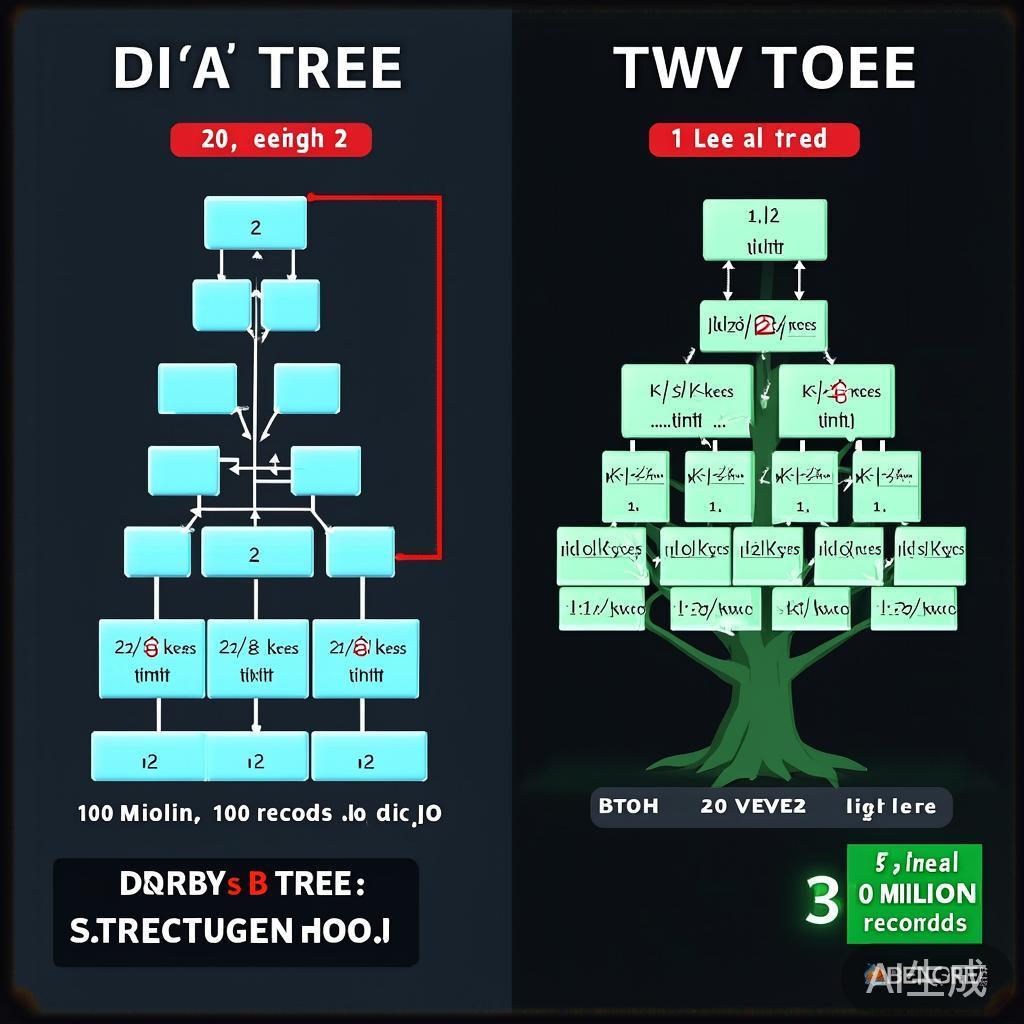
图1:二叉树vs B树结构对比 – 相同数据量下的树高差异
节点约束:
阶数 m = 5
最多键数 = m-1 = 4
最多子节点 = m = 5
最少键数(非根)= ⌈5/2⌉-1 = 2
最少子节点(非根)= ⌈5/2⌉ = 3
示例节点:
[P₀|10|P₁|20|P₂|30|P₃|40|P₄]
解读:
- 4个键:10, 20, 30, 40
- 5个指针:P₀, P₁, P₂, P₃, P₄
- P₀子树:所有键 < 10
- P₁子树:10 < 键 < 20
- P₂子树:20 < 键 < 30
- P₃子树:30 < 键 < 40
- P₄子树:所有键 > 40
📐 数学原理:阶数与树高的关系
树高计算公式
对于N个键的m阶B树,树高h的计算:
h = ⌈log_m(N)⌉
其中:
- N = 总记录数
- m = B树的阶数(每节点最多m个子节点)
- h = 树的高度(层数)
实际案例计算
场景: 数据库有 1,000,000 条用户记录
案例1:使用100阶B树
m = 100(每节点最多100个子节点)
h = ⌈log₁₀₀(1,000,000)⌉
= ⌈log(1,000,000) / log(100)⌉
= ⌈6 / 2⌉
= 3
查询成本:
- 最多磁盘I/O次数 = 3次
- HDD延迟 = 3 × 10ms = 30ms
- SSD延迟 = 3 × 100μs = 0.3ms
案例2:使用1000阶B树
m = 1000(每节点最多1000个子节点)
h = ⌈log₁₀₀₀(1,000,000)⌉
= ⌈log(1,000,000) / log(1000)⌉
= ⌈6 / 3⌉
= 2
查询成本:
- 最多磁盘I/O次数 = 2次
- HDD延迟 = 2 × 10ms = 20ms
- SSD延迟 = 2 × 100μs = 0.2ms
不同阶数的性能对比
| 阶数m | 100万记录树高 | 1000万记录树高 | 1亿记录树高 |
|---|---|---|---|
| 10 | 6 | 7 | 8 |
| 100 | 3 | 4 | 4 |
| 200 | 3 | 3 | 4 |
| 500 | 2 | 3 | 3 |
| 1000 | 2 | 3 | 3 |
关键洞察:
– 阶数从10增加到100,树高减半
– 阶数从100增加到1000,收益递减
– 实践中m=200-500是性价比最优选择
🔎 B树查询算法详解
查询流程伪代码
def search_btree(node, key):
"""
在B树中查找键值
参数:
node: 当前节点
key: 要查找的键
返回:
(找到的记录, I/O次数)
"""
io_count = 1 # 读取当前节点 = 1次I/O
# 在当前节点的键数组中查找
i = binary_search(node.keys, key)
# 情况1:找到键
if i < len(node.keys) and node.keys[i] == key:
return (node.values[i], io_count)
# 情况2:到达叶子节点但未找到
if node.is_leaf:
return (None, io_count)
# 情况3:递归到子节点继续查找
child = load_from_disk(node.pointers[i]) # 又1次I/O
result, child_io = search_btree(child, key)
return (result, io_count + child_io)
查询过程可视化
查询示例: 在5阶B树中查找键值 25
第1步(根节点):读取根节点 [20|40|60]
→ 25 > 20 且 25 < 40
→ 沿着P₁指针向下
I/O次数 = 1
第2步(中间节点):读取节点 [22|25|30|35]
→ 找到键25!
→ 返回对应的数据记录
I/O次数 = 2
总成本:
- 磁盘I/O:2次
- 内存二分查找:每节点O(log m)
- 总时间复杂度:O(h × log m) = O(log_m(N) × log m) = O(log N)
查询键 78 的过程:
第1步(根节点):[20|40|60]
→ 78 > 60
→ 沿P₃向下
I/O = 1
第2步(中间节点):[65|70|75|80]
→ 78 > 75 且 78 < 80
→ 沿P₃向下
I/O = 2
第3步(叶子节点):[76|77|78|79]
→ 找到78
I/O = 3
💾 磁盘块对齐优化
为什么要对齐磁盘页?
磁盘I/O的基本单位是页(Page):
操作系统磁盘I/O:
- 读取最小单位 = 1个页(4KB/8KB/16KB)
- 即使只需1字节,也要读取整个页
B树的设计策略:
让B树节点大小 = 磁盘页大小
这样每次I/O都充分利用带宽,不浪费
节点大小计算
假设:
– 磁盘页大小 = 8KB = 8192 字节
– 键大小 = 8字节(int64)
– 指针大小 = 8字节(内存地址/磁盘偏移)
– 值大小 = 128字节(记录摘要/指向完整记录的指针)
节点结构大小计算:
对于m阶B树的满节点:
键数量 = m - 1
指针数量 = m
值数量 = m - 1
节点大小 = (m-1)×8 + m×8 + (m-1)×128
= 8m - 8 + 8m + 128m - 128
= 144m - 136 字节
要求节点 ≤ 8192字节:
144m - 136 ≤ 8192
144m ≤ 8328
m ≤ 57.8
最优选择:m = 57
实际节点大小:
m = 57时:
节点大小 = 144×57 - 136 = 8072字节
剩余空间 = 8192 - 8072 = 120字节(可用于元数据)
每个节点:
- 最多56个键
- 最多57个指针
- 最多56个值
真实数据库配置
MySQL InnoDB的B+树:
默认页大小 = 16KB
索引键 + 指针 ≈ 14字节
每页约可存 16384/14 ≈ 1170 个键
阶数 m ≈ 1170
树高计算(1亿记录):
h = log₁₁₇₀(100,000,000) ≈ 3层
实际查询:
- 根节点常驻内存(0次I/O)
- 中间层可能缓存(0-1次I/O)
- 叶子层必定I/O(1次I/O)
平均I/O次数 ≈ 1-2次!
PostgreSQL的B-tree:
默认页大小 = 8KB
阶数 m ≈ 300-500(取决于键类型)
支持自定义页大小(1KB到32KB)
🎯 实践建议
选择合适的阶数
权衡因素:
- 磁盘页大小
- 现代SSD:4KB页
- 传统HDD:512字节扇区
-
数据库页:4KB-16KB
-
键值大小
- 整数键:8字节 → 可以更大的m
- 字符串键:可变长度 → 需要更小的m
-
复合键:多列组合 → 根据总大小计算
-
内存开销
- 阶数越大,节点越大
- 缓存命中率可能降低
- 需要平衡I/O次数与缓存效率
推荐配置:
通用场景:m = 200-500
整数索引:m = 500-1000
字符串索引:m = 100-300
复合索引:m = 50-200
🔗 系列导航
- ← 上一篇:磁盘I/O危机 – 理解问题的根源
- 当前:B树基础 – 掌握解决方案的核心
- → 下一篇:B树维护 – 学习插入删除的平衡算法
✅ 本篇检查清单
在继续下一篇前,请确保你理解:
- [ ] B树用”胖节点”降低树高的核心思想
- [ ] 阶数m的定义和节点容量约束
- [ ] 树高h = log_m(N)的数学原理
- [ ] 为什么100万记录只需3次I/O
- [ ] B树查询算法的完整流程
- [ ] 节点大小与磁盘页对齐的优化原理
- [ ] 如何根据磁盘页大小和键大小计算最优阶数
理解度自测:
如果有一个1000万记录的数据库,使用500阶B树,树高是多少?需要几次磁盘I/O?
点击查看答案
h = ⌈log₅₀₀(10,000,000)⌉
= ⌈log(10,000,000) / log(500)⌉
= ⌈7 / 2.699⌉
= ⌈2.59⌉
= 3
需要3次磁盘I/O(根节点、1个中间节点、1个叶子节点)
下一篇预告: 我们将深入B树的动态维护算法 —— 如何在插入和删除时保持树的平衡性和阶数约束,这是B树最精巧的设计部分!






 AI周刊:大模型、智能体与产业动态追踪
AI周刊:大模型、智能体与产业动态追踪 程序员数学扫盲课
程序员数学扫盲课 冲浪推荐:AI工具与技术精选导航
冲浪推荐:AI工具与技术精选导航 Claude Code 全体系指南:AI 编程智能体实战
Claude Code 全体系指南:AI 编程智能体实战
最新评论
Flash版本的响应速度确实提升明显,但我在使用中发现对中文的理解偶尔会出现一些奇怪的错误,不知道是不是普遍现象?
遇到过类似问题,最后发现是网络环境的问题。建议加一个超时重试机制的示例代码。
谢谢分享,我是通过ChatGPT的索引找到这里来的。
十年打磨一个游戏确实罕见,这种专注度在快节奏的游戏行业很难得。从Braid到The Witness,每作都是精品。
快捷键冲突是个很实际的问题,我自己也被这个问题困扰过。最后通过自定义快捷键组合解决了。
会议摘要这个功能很实用,特别是对经常需要参加长会议的人。不过三次免费使用确实有点少了。
硕士背景转AI基础设施,这个路径其实挺常见的。建议多关注底层系统知识,而不只是模型应用层面。
配置虽然简单,但建议补充一下认证和加密的注意事项,避免被中间人攻击。