Karpathy神经网络05：反向传播 - 徒手写梯度

本文是《Karpathy神经网络零基础课程》系列文章

← 上一篇：Karpathy神经网络04：BatchNorm – 解决训练崩盘 | → 下一篇：Karpathy神经网络06：WaveNet – 神经网络大升级

这是一篇为你准备的、关于这期硬核AI视频的详细学习笔记。这篇文章假设你是一个对人工智能充满好奇的初中生，我们将一起拆解”神经网络是如何学习的”这一核心秘密，也就是反向传播（Backpropagation）。

【AI进阶课】像忍者一样掌握”反向传播”：揭开神经网络学习的黑盒

你好！如果你以前玩过神经网络，或者看过Andrej Karpathy之前的视频，你可能知道我们在训练AI时，通常只需要按下一个”魔法按钮”——在PyTorch代码里，它叫 loss.backward()。按下它，计算机会自动算出如何调整网络参数，让AI变得更聪明。

但是，如果这个魔法按钮坏了怎么办？ 或者如果我想创造一种没人见过的新型AI，现有的魔法不管用了怎么办？

在这堂课（MakeMore 第4期）中，Karpathy老师带我们通过“徒手写代码”的方式，不依赖任何自动工具，从零实现那个魔法按钮的功能。我们将从一个普通的“调包侠”进化为一名反向传播忍者（Backprop Ninja）。

第一部分：为什么要这么做？（Leaky Abstractions）

你可能会问：“既然电脑能自动算，为什么我要自己算？”

Karpathy老师提出了一个概念叫泄漏的抽象（Leaky Abstractions）。意思是，虽然现在的工具（如PyTorch）把复杂的数学封装得很完美，但如果你不理解它内部的原理，一旦遇到Bug（比如梯度消失、梯度爆炸，或者训练死机），你就完全束手无策。

学习目标：通过手动推导每一个步骤的梯度，彻底理解神经网络内部的数据是如何流动的。

第二部分：核心武器——链式法则（Chain Rule）

这堂课的核心数学工具其实只有一个：链式法则。
别被名字吓到，它的逻辑很简单：

如果你想知道由于A的变化导致C变化了多少，你可以先算A的变化如何影响B，再算B的变化如何影响C，然后把这两个影响乘起来。

在神经网络中，每一层都在做这个传递游戏。

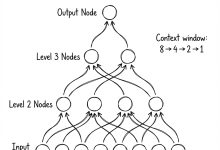
• 前向传播（Forward Pass）：数据从输入 -> 隐层 -> 输出 -> 损失（Loss）。
• 反向传播（Backward Pass）：我们也叫它“求导”或“算梯度”。我们要从最后的 Loss 开始，一步步往前推，算出每一个参数对 Loss 的“贡献”有多大。

第三部分：实战演练——通关四个关卡

视频中，我们将整个过程分成了四个练习（Exercise），就像游戏的四个关卡。

关卡 1：显微镜下的反向传播 (Micro-Level)

我们之前写的神经网络里，Loss的计算是一行代码搞定。但在这一关，我们要把它打碎。
比如计算“对数概率”这个步骤，本来是一步，现在我们把它拆成：

1. 挑出正确的概率
2. 取对数
3. 取负数
4. 求平均

核心技巧：

• 局部求导 × 全局梯度：对于每一个微小的操作（比如加法、乘法、log），我们先算出它自己的导数（局部），然后乘以上一步传回来的梯度（全局）。
• 形状（Shape）是关键：这是调试代码的秘诀。如果你不知道梯度怎么算，先看张量的形状（比如是 32x64 还是 64x27）。梯度的形状通常必须和原始数据的形状完全一致。

一个重要的发现：
如果在前向传播中，你把一个数字复制（Replicate/Broadcast）多次使用；那么在反向传播时，你需要把这些地方回传的梯度加起来（Sum）。

记忆口诀：前向广播（Broadcast），反向求和（Sum）。

关卡 2：数学的胜利 (Cross Entropy Loss)

在关卡1里，我们把 Loss 拆得太细了，算起来很累。其实，数学家们已经帮我们推导出了一个超级简洁的公式。

对于最常用的交叉熵损失（Cross Entropy Loss），它的梯度计算结果极其优雅：

• 直觉理解：想象神经网络是一个巨大的滑轮组。
• 对于正确的答案，我们要提升它的概率（Pull up）。

• 对于错误的答案，我们要压低它的概率（Pull down）。

• 直觉理解：想象神经网络是一个巨大的滑轮组。

• 对于正确的答案，我们要提升它的概率（Pull up）。

• 对于错误的答案，我们要压低它的概率（Pull down）。

• 力的大小：你预测得越错，受到的“拉力”就越大。

通过手推公式，我们发现不需要写十几行代码，只需要两三行就能算出最终的梯度，而且运行速度更快！

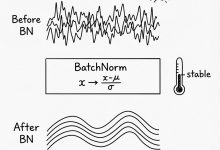
关卡 3：大Boss——批量归一化 (Batch Normalization)

这是最难的一关。Batch Normalization (BatchNorm) 视频地址**：https://www.youtube.com/watch?v=q8SA3rM6ckI 是现代深度学习中非常常用但也非常复杂的层。

它涉及计算均值、方差，然后把数据标准化，再缩放和平移。
Karpathy老师在纸上画出了详细的计算图（Computational Graph），一步步推导。

给初中生的简化理解：
想象你有32个学生（一个Batch）的成绩。BatchNorm 就是把大家的分数变成“距离平均分几个标准差”。
在反向传播时，因为每个人的分数都参与了计算平均分，所以修改一个人的分数，会影响平均分，进而影响所有人的最终得分。这个相互纠缠的关系，使得计算梯度时非常麻烦，需要把所有相关的路径都加起来。

虽然公式很长，但只要耐心运用链式法则，一定能解出来！

关卡 4：成为忍者 (Putting it all together)

在这个关卡，我们将把之前手写的：

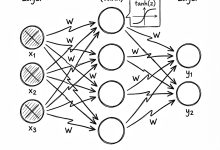
• 线性层（Linear Layer）的梯度
• 激活函数（Tanh）的梯度
• 批量归一化（BatchNorm）的梯度
• 损失函数（Cross Entropy）的梯度

全部拼装在一起，**完全抛弃 PyTorch 的 loss.backward()**。

结果呢？我们训练出的网络效果和用自动工具训练的一模一样！这意味着我们彻底搞懂了黑盒里的每一个齿轮。

第四部分：课后总结与细节贴士

1. 矩阵乘法的反向传播：
   当你做矩阵乘法 时，A的梯度其实是 。如果你记不住公式，看维度（Shape）就能推导出来，只有转置后维度才能对得上！
2. 贝塞尔校正 (Bessel’s Correction)：
   视频中提到了一个细节，计算方差时是用 还是 ？虽然在很多库里混用了，但数学上用 是“无偏估计”，更准确。这告诉我们要对细节保持敏感。
3. 调试技巧：
   Karpathy老师写了一个 cmp 函数，用来比较“我们手算的梯度”和“PyTorch自动算的梯度”。如果两者误差极小（比如 ），说明我们算对了。这就是科学精神——大胆假设，小心求证。

结语

通过这节课，你不再是一个只会调用函数的“调包侠”。你现在能够看到神经网络每一行代码背后数据的流动。正如Karpathy所说，当你理解了这些原理，你就是一名Backprop Ninja，任何Bug都无法在你的显微镜下遁形！

现在的你，准备好拿起纸笔，去推导那些公式了吗？

返回系列总览

👉 Karpathy神经网络零基础课程：完整课程大纲